1. 우선순위 큐
- 우선순위 큐는 각 원소들이 우선순위를 갖고 있는 추상 자료형이다.
- FIFO 구조를 갖는 큐와 다르게 우선순위 큐는 들어온 순서와 상관없이 우선순위가 높은 원소가 먼저 나간다.
- 원소를 추가하거나 제거할 때 우선순위를 갖고 수행해야 한다.
- 우선순위 큐와 힙은 같지 않다. 우선순위 큐는 힙 외에도 배열이나 연결 리스트로도 구현 가능하다.
- 배열을 이용해 우선순위 큐를 구현하면 삽입할 때 최악의 경우 시간 복잡도가 O(N)이 된다.
(추가하는 위치 이후에 있는 모든 원소들을 뒤로 한 칸씩 옮겨줘야 하기 때문에)
- 연결리스트로 구현할 때도 삽입 위치를 찾을 때 최악의 경우 O(N)이 소요되기 때문에 배열이나 연결 리스트보다는 힙을 이용한 우선순위 큐가 훨씬 효율적이다.
2. 힙을 이용한 우선순위 큐 구현
- 여기서는 최소 힙을 구현해 보려 한다.
- 매번 힙의 루트를 내보내는 형태로 우선순위 큐를 구현할 수 있다.
- heappush 연산을 한 후에 모든 부모 노드가 자식 노드보다 우선순위가 높도록 순서를 바꿔준다.
- heappop 연산을 통해 루트 노드를 내보내고 힙에 있는 나머지 원소들 중 우선순위가 가장 높은 원소를 루트 노드가 되도록 순서를 바꿔준다.
1) 우선순위 큐 선언
class PriorityQueue(object):
def __init__(self):
self.items = [None]
def __len__(self):
return len(self.items) - 1
def __repr__(self):
return ' '.join(map(str, self.items[1:]))힙은 완전 이진트리로 리스트를 이용해 표현 가능하다. 여기서 사용하는 리스트는 완전 이진트리를 구현한 것으로 배열을 사용한 우선순위 큐 구현과는 다르다.
- items는 완전이진트리로 0번 인덱스를 사용하지 않고 1번 인덱스부터 사용할 것이다.
- items는 None을 원소로 포함하고 있으므로 반환하는 길이는 items - 1로 한다.
- 값을 확인하기 위해 repr을 정의해주고 0번 인덱스인 None을 제외하고 반환하도록 한다.
2) heappush
- 우선 힙의 가장 마지막 레벨의 가장 왼쪽 노드의 원소를 삽입한다. (완전 이진트리 구조이므로)
- 부모 노드와 비교해 추가된 노드가 부모 노드보다 값이 작다면 부모 노드와 순서를 바꿔준다.
- 루트 노드까지 위 연산을 반복한다.
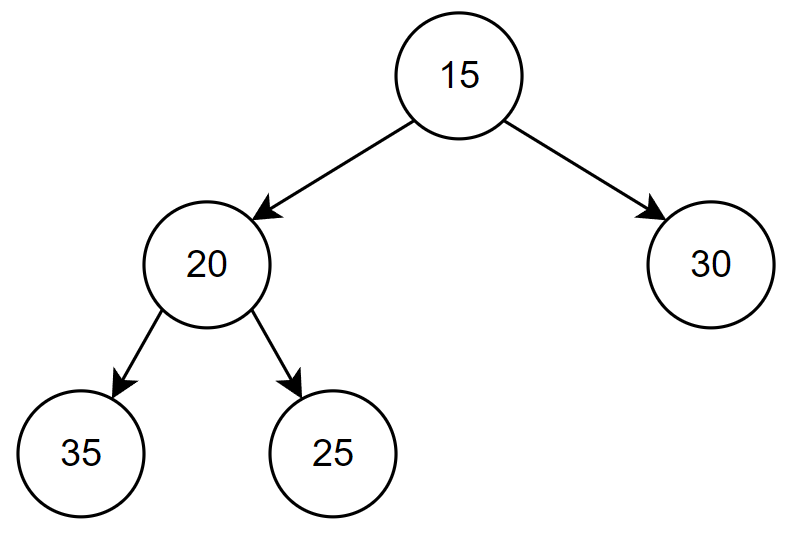





최종적으로 값이 추가된 우선순위 큐는 다음과 같이 힙 구조를 유지한다.

def _percolate_up(self):
i = len(self)
parent = i // 2
while i > 1:
if self.items[parent] > self.items[i]:
self.items[parent], self.items[i] = self.items[i], self.items[parent]
i = parent
parent //= 2
def heappush(self, item):
self.items.append(item)
self._percolate_up()
3) heappop
- 힙은 루트 노드가 우선순위가 가장 높으므로 pop연산을 하면 루트 노드를 반환한다.
- 힙의 가장 아래, 가장 오른쪽 원소를 힙의 루트 노드로 올려준다.
- 이렇게 하는 이유는 힙의 완전 이진트리 형태를 유지해 주기 위함이다.
- 루트 노드부터 시작해 자식노드와 우선순위를 비교해 두 자식 중 우선순위가 높은 자식 노드와 위치를 바꾼다.
- 최소힙의 경우 값이 작은 자식 노드가 우선순위가 더 높다.






최종적으로 최소 힙은 루트 노드인 9를 반환하고 다음과 같이 최솟값을 루트 노드로 올려 상태를 유지한다.

def _percolate_down(self, idx=1):
left, right = idx << 1, idx << 1|1
smallest = idx
if left < len(self) and self.items[left] < self.items[smallest]:
smallest = left
if right < len(self) and self.items[right] < self.items[smallest]:
smallest = right
if smallest != idx:
self.items[idx], self.items[smallest] = self.items[smallest], self.items[idx]
self._percolate_down(smallest)
def heappop(self):
extracted = self.items[1]
self.items[1] = self.items[-1]
self.items.pop()
self._percolate_down()
return extracted3. 예제 코드
class PriorityQueue(object):
def __init__(self):
self.items = [None]
def __len__(self):
return len(self.items) - 1
def __repr__(self):
return ' '.join(map(str, self.items[1:]))
def _percolate_up(self):
i = len(self)
parent = i // 2
while i > 1:
if self.items[parent] > self.items[i]:
self.items[parent], self.items[i] = self.items[i], self.items[parent]
i = parent
parent //= 2
def heappush(self, item):
self.items.append(item)
self._percolate_up()
def _percolate_down(self, idx=1):
left, right = idx << 1, idx << 1|1
smallest = idx
if left < len(self) and self.items[left] < self.items[smallest]:
smallest = left
if right < len(self) and self.items[right] < self.items[smallest]:
smallest = right
if smallest != idx:
self.items[idx], self.items[smallest] = self.items[smallest], self.items[idx]
self._percolate_down(smallest)
def heappop(self):
extracted = self.items[1]
self.items[1] = self.items[-1]
self.items.pop()
self._percolate_down()
return extracted
q = PriorityQueue()
nums = [15, 20, 30, 35, 25]
for num in nums:
q.heappush(num)
print('초기 priority queue')
print(q)
q.heappush(9)
print('\nheappush 연산 후 priority queue')
print(q)
print('\nheappop 연산 후 priority queue')
print('\nheappop 반환값: ', q.heappop())
print(q)
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 힙(Heap) (0) | 2022.03.15 |
|---|---|
| [Python] 트리 구현 / 순회(전위 순회, 중위 순회, 후위 순회, 레벨 순회) (0) | 2022.03.11 |
| [자료구조] 트리(Tree) (5) | 2021.04.24 |
| [Python] 큐 구현 (0) | 2021.04.24 |
| [Python] 이중 연결리스트 구현 (1) | 2021.04.24 |