1. 테일러급수(Taylor Series)

테일러급수는 무한히 미분 가능한 함수 f(x)에 대해 점 x=a에서 해당 함수 f(x)에 접하는 다항 함수를 표현하는 방법이다.
테일러급수는 말 그대로 급수로, 무한개의 다항식으로 표현된다. 하지만 몇 개의 항만을 이용해도 해당 값에 근사한 값을 구할 수 있으므로 보통 몇 개의 항만을 이용해 근사치를 낸다.
테일러급수를 이용하면 해석 함수의 근사치를 구할 수 있다. 삼각함수나 지수함수들도 다항함수로 나타내 값을 근사 시킬 수 있고 외에도 복잡한 해석 함수 계산도 비교적 쉽게 구할 수 있는 장점이 있다.
테일러급수가
a=0인 경우의 테일러급수가 주로 사용되고 이런 급수를 매클로린 급수라 한다.
2. 테일러급수의 증명
무수히 미분 가능한 함수 y=f(x)에 대해, 함수 f(x)는 다음을 만족한다.

f(a)를 제외하고 뒤에 있는 적분식을 부분 적분을 이용해 계산해보자


다시 뒤에 있는 적분식만 살펴보면,

마지막으로 한 번 더 뒤의 적분식을 계산하면,

위 식들을 정리해서 f(x)를 나타내 보자

마지막 적분식은 위에서와 같이 계속 적분이 가능하다. 식을 계속 정리해 나가면 위의 테일러급수를 구할 수 있다


3. 매클로린 급수(Maclaurin Series)
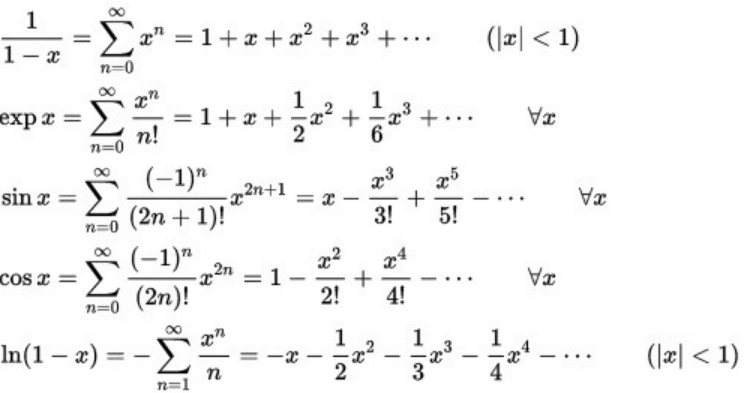
'Math' 카테고리의 다른 글
| 오일러 공식(Euler's formula) (0) | 2022.10.11 |
|---|---|
| 내가 보려고 정리하는 미/적분학 공식 (0) | 2022.09.17 |
| 분수함수 미분, 목의 미분 (0) | 2022.09.16 |
| [Matplotlib] 시그모이드 함수 그리기 (0) | 2022.08.10 |
| 시그모이드 함수(Sigmoid Function) (0) | 2020.09.30 |