1. pandas.crosstab
crosstab은 범주형 변수를 기준으로 데이터의 개수를 파악할 때 사용합니다. crosstab을 사용해 빈도표를 만들어 카이제곱검정을 할 때도 유용합니다.
| 파라미터 | 설명 |
| index: array-like, Series,list, arrays | 행으로 지정할 데이터 |
| columns: array-like, Series, list, arrays | 열로 지정할 데이터 |
| values: array-like, optional | 집계할 데이터 (aggfunc을 같이 사용해야 합니다) |
| aggfunc: function, optional | 집계할 방법을 선택(count, mean, median ...) |
| margins: bool, default=False | 총계를 보고 싶은 경우 사용 |
| dropna: bool, default=True | Nan값을 포함하지 않을지 여부 |
| rownames: sequence, default=None | 행 이름 설정 |
| colnames: sequence, default=None | 열 이름 설정 |
| margins_name: str, default='All' | 총계(margin) 이름 설정 |
| normalize: bool, {all, index, columns}, default=False | 정규화 여부 - all: 전체 데이터를 정규화 - index: 각 행에 따라 정규화 - columns: 각 열에 따라 정규화 |
① 기본 사용 방법
import seaborn as sns
import pandas as pd
data = sns.load_dataset('tips')
pd.crosstab(data.day, data.time)
범주형 변수들을 넘기면 이에 따른 빈도표를 생성해줍니다.
index에 2개의 categoric 변수를 넘겨주면 n중 index를 사용해 빈도표를 생성합니다.
pd.crosstab([data.day, data.time], data.smoker)
pd.crosstab([data.day, data.time, data.smoker], data.sex)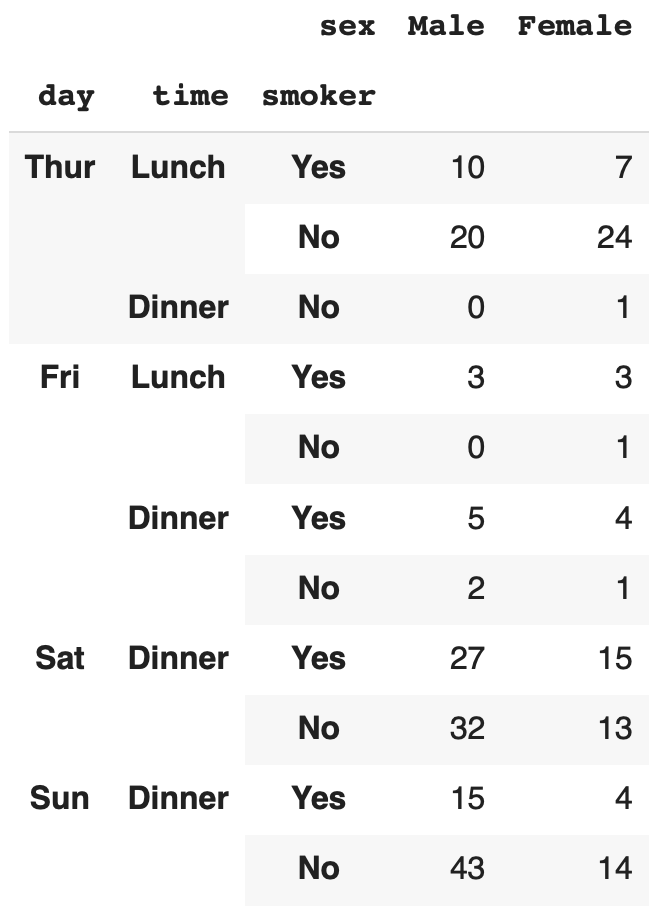
2. scipy.stats.chi2_contingency
chi2_contingency는 빈도표가 주어지면 빈도표를 이용해 카이제곱분포값과 p-value, dof(자유도) 그리고 기대빈도를 반환합니다.
crosstab을 이용해 얻은 빈도표를 chi2_contingency의 입력값으로 사용하면 바로 카이제곱분포를 사용할 수 있어 편합니다.
| 파라미터 | 설명 |
| observed: array-like | table을 입력받음, R x C Table을 입력 |
| correction: bool, optional | correction=True이고 dof=1 (ex. 2 x 2 분할표)이라면 Yates' correction을 적용 |
| 반환값 | 설명 |
| chi2: float | chi2통계량 |
| p: float | p-value |
| dof: int | 자유도 (degree of freedom) |
| expected: ndarray, same shape as observed | 기대 분포표 |
import seaborn as sns
import pandas as pd
from scipy.stats import chi2_contingency
data = sns.load_dataset('tips')
chi2, p, dof, expected_ = chi2_contingency(pd.crosstab(data.day, data.time))
print('chi2 statistic: ', chi2)
print('p value: ', p)
print('dof: ', dof)
print('expected frequency')
print(expected_)

chi2_contingency는 순서대로 검정통계량, p value, dof, 기대분포표를 반환합니다.
p value: 95% 신뢰수준에서 α > p-value로, 귀무가설을 기각, 동일한 분포를 따르지 않을 것임을 알 수 있습니다.
빈도표(분할표)의 크기는 4 x 2로, 자유도는 (4 - 1) x ( 2 - 1) = 3임을 알 수 있습니다.기대분포표에 대해서는 카이제곱분포를 정리하면서 다시 한 번 정리해보겠습니다.통계적 유의성을 판단할 때는 검정통계량이나 p-value를 이용해, 충분히 귀무가설을 기각할 수 있기 때문에 기대분포표에 대해서는 별도 게시물에 정리하겠습니다!
'Python > Syntax' 카테고리의 다른 글
| [Python] itertools (순열, 조합) (0) | 2022.12.21 |
|---|---|
| [Pandas] pivot (0) | 2022.09.28 |
| [Python] Dictionary 대신 사용할 수 있는 dataclass (0) | 2022.09.10 |
| [Python] Dictionary 대신 사용할 수 있는 NamedTuple (NamedTuple Type Annotation) (0) | 2022.09.10 |
| [colab] colab에서 ipynb파일 import하기 (0) | 2022.09.02 |