전에 파이썬의 bisect 라이브러리의 bisect_left와 bisect_right을 다룬 적이 있었습니다. 그 때는 기본적인 함수의 동작방식과 사용방법에 대해서만 공부해봤는데 최근에 LIS 문제를 다시 풀어보면서 lower bound를 다시 공부할 기회가 생겼었습니다. 오늘은 직접 bisect_left, bisect_right를 구현해보려 합니다.
오늘 게시물을 보기 전에 아래 게시물에서 lower bound와 upper bound에 대해 읽어보고 오시길 추천드립니다.
간단하게
lower bound: target "이상(target 포함o)"이 처음 나오는 위치
upper bound: target"보다 큰(target 포함x)" 값이 처음 나오는 위
[Python] bisect 라이브러리 (lower bound, upper bound)
bisect 라이브러리에 있는 bisect_left, bisect_right에 대해 공부하려 합니다. 1. bisect? - 정렬된 리스트에서 이진 탐색을 이용해 데이터를 찾는 메서드를 제공 - O(logN)의 시간 복잡도로 데이터를 찾을 수
koosco.tistory.com
lower bound와 upper bound함수는 이진탐색과 비슷한 형태를 갖고 있지만
1. target이 되는 값이 없더라도 반환값을 반환
2. 해당하는 값이 여러개가 있어도 반환값을 반환
3. mid와 target이 같은 경우 어떻게 처리할지에 따라 lower bound, upper bound로 나뉘게 된다
위 3가지에 유의하여 코드를 작성해보려 합니다.

nums와 target은 위와 같이 주어지는 경우에 대해 적용해보겠습니다.
1. lower bound (bisect left)
lower bound의 결과는 target 이상의 값이 처음 나오는 위치이므로, 반환값은 20이 처음 나오는 1이 됩니다.
1)

20 이상이 처음 나오는 위치를 구해야하므로 target과 nums[mid]의 값이 같은 경우 right = mid로 설정
(right = mid -1로 설정할 경우 mid 위치에 있는 값이 제외되므로 right 또는 left의 값 중 하나가 mid를 포함해야합니다.
저는 right가 mid를 포함하도록 코드를 작성해보겠습니다)
위 과정을 계속 반복하면 다음과 같습니다
2)

3)

4)
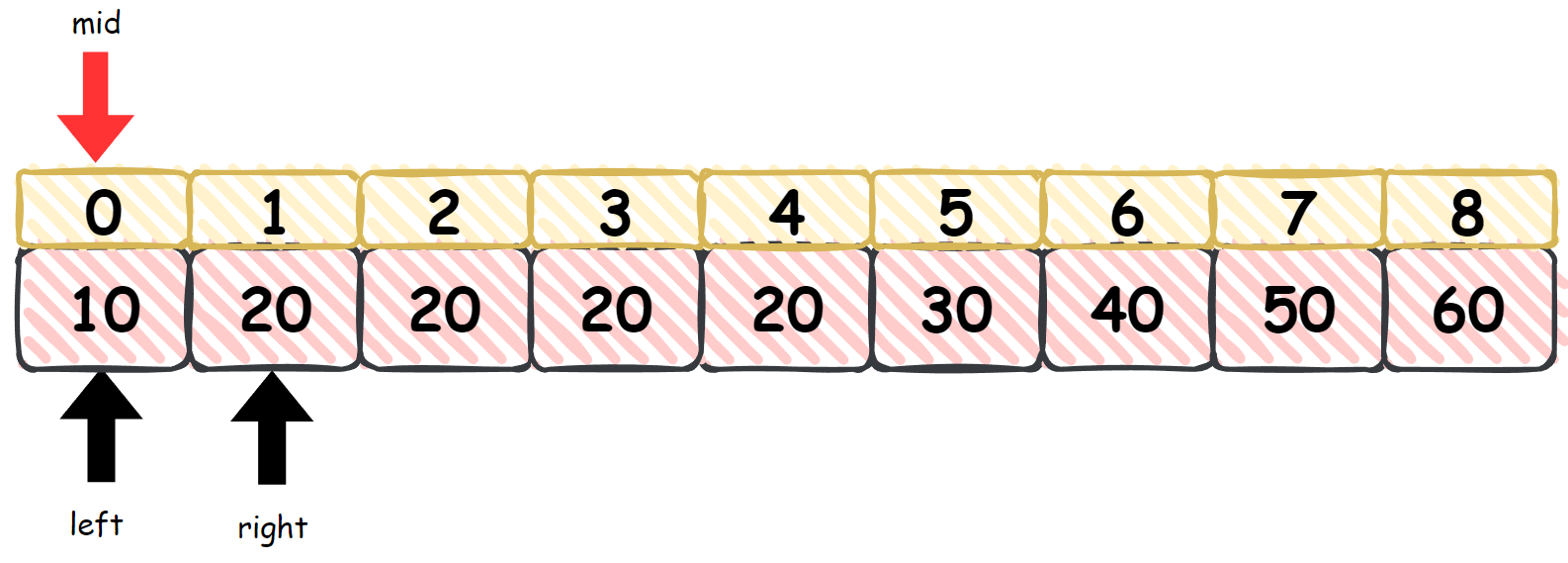
5)

left가 right 이상이 되면 loop를 멈추고 left와 right 중 하나를 반환합니다.
from typing import List
def lower_bound(nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
else:
right = mid
return left2. upper bound (bisect right)
1)

upper bound도 lower bound와 동일하게 시작합니다. 하지만 upper bound의 경우 lower bound와 다르게 해당하는 값보다 큰 값을 반환해야하기 때문에 nums[mid]와 target이 같은 경우 mid보다 오른쪽을 탐색해야 합니다.
그러므로 nums[mid]와 target이 같은 경우, left = mid + 1로 해줍니다.
left = mid + 1 로 설정하는 이유는 left = mid 인 경우 무한 루프가 되기 때문에 left와 right의 값을 마지막에 같게 해주기 위함입니다.
2)

3)

4)

from typing import List
def upper_bound(nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] <= target:
left = mid + 1
else:
right = mid
return left
둘 모두 마지막에 left와 right의 값이 같아지기 때문에 반환값으로 둘 중 무엇을 써도 상관없습니다.
lower bound를 사용하면 최솟값을 O(log(N))으로 찾을 수 있기 때문에 선형탐색에 비해 매우 유용합니다!
다만 이진 탐색과 마찬가지로 자료의 정렬을 필요로 하기 때문에 이 점을 유의해서 사용하면 될 것 같습니다.
다음은 lower bound를 이용해서 O(N^2)의 LIS 알고리즘 문제를 O(Nlog(N))으로 풀어보려 합니다!
'CS > 알고리즘' 카테고리의 다른 글
| 유클리드 호제법 (0) | 2023.01.11 |
|---|---|
| 배수판정법 (1) | 2023.01.10 |
| [Python] 피보나치 수열과 Dynamic Programming 기초 (0) | 2022.03.19 |
| [Python] bisect 라이브러리 (lower bound, upper bound) (0) | 2022.03.19 |
| [Python] 이진탐색(Binary Search) (0) | 2022.03.13 |