1. 단순선형회귀
회귀는 문제를 예측할 때 사용하는 알고리즘이다. 입력값과 출력 값이 주어질 때, 이에 대한 함수를 정의하고 새로운 데이터가 들어왔을 때, 정의된 함수를 이용해 값을 예측하도록 동작한다.
X = [1, 2, 3]
Y = [5, 8, 11]위와 같이 x와 y값이 주어졌을 때, 우리는 x와 y의 관계가 y = 3x + 2라고 직감적으로 유추할 수 있다.
동일한 관계로 3개의 값이 주어졌을 때는 쉽게 유추할 수 있다. 하지만 데이터의 수가 많아지고 데이터들이 동일한 직선 위에 존재하지 않는다면 직관적으로 관계를 유추하기 어려워진다. 선형회귀는 많은 데이터가 주어졌을 때, 데이터들의 관계를 가장 잘 나타내는 함수를 표현하는 방법이다.
단순선형회귀는 독립변수가 하나일 때의 회귀식으로 일차원 그래프를 갖게 된다.

이때 w1을 가중치(기울기), w0는 y축 절편이다. 단순선형회귀의 목표는 데이터들의 관계를 가장 잘 나타내는 w1(기울기)와 w0(y축 절편)을 찾는 것이다.
2. 손실함수
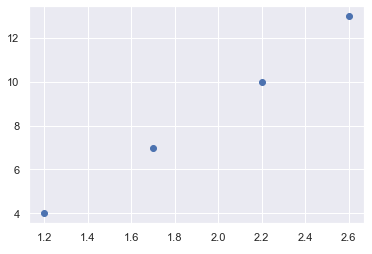
위와 같은 데이터가 주어졌을 때, 데이터에 가까운 임의의 직선을 그릴 수 있다.

우리는 주어진 데이터를 가장 잘 나타내는 직선을 원한다. 데이터를 가장 잘 나타내기 위해서는 먼저 이 직선이 얼마나 큰 오차를 갖고 있는지를 확인하고 오차를 줄여나가는 방식으로 식을 수정해 나가야 한다.
평균제곱오차를 사용하면 직선과 데이터가 평균적으로 얼마나 떨어져 있는지 확인할 수 있다.
평균제곱오차는 주어진 직선과 주어진 데이터의 y축 거리를 계산한 후 제곱한 값들의 평균을 계산해 얻을 수 있다.
평균제곱오차를 나타내는 식을 손실함수라 하고 식으로 나타내면 다음과 같다.

오차를 계산할 때 제곱을 이용하지 않고 절댓값을 이용할 수도 있지만 제곱을 이용하면 크게 두 가지 이점이 있다.
- 제곱을 이용하면 손실값이 더 커진다. 손실값이 크면 그만큼 빠르게 학습이 가능하다.
- 절댓값을 구현하면 조건문이 필요하기 때문에 연산속도가 느려질 수 있다. 부호에 상관없이 제곱을 하면 별도의 조건문이 필요하지 않다.
3. 손실함수의 최적화(평균제곱오차의 최소화)
손실함수에서 x와 y값들은 주어지는 데이터이다. 이미 주어진 값들이므로 x와 y는 상수로 생각하고 기울기와 절편을 변수로 취급한다.
1) 기울기의 오차함수
오차가 줄어드는 방향으로 기울기를 움직이면 오차는 점점 줄어들 것이다. 하지만 기울기를 너무 많이 움직이면 오차는 줄어들다가 다시 증가하게 된다. 즉, 단순선형회귀에서 기울기에 따른 손실값은 2차 함수 형태를 띤다.

우리는 기울기에 따른 손실이 최소가 되는 순간을 구하고 싶다. 즉, 기울기-손실값함수의 최솟값(미분값이 0이 되는 순간)을 구하는 것을 목표로 한다.
2) y축 절편의 오차함수
기울기와 마찬가지로 y축 절편을 데이터에 가깝게 움직이다 보면 오차는 점점 줄어든다. 하지만 너무 많이 움직이면 오차는 다시 증가하므로 2차 함수 형태를 띤다.

마찬가지로 절편-손실값함수의 최솟값을 구하고 싶다.
기울기와 y축 절편에 따른 손실함수의 최솟값을 구하고 싶으므로 편미분을 이용해 기울기를 구할 수 있다.
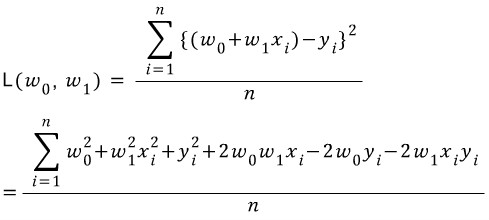
편미분값을 계산하면 다음과 같다.
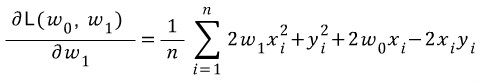
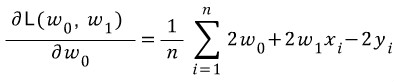
편미분식을 구한 후 손실값이 0에 수렴할 때까지 각각 기울기와 y절편에서 해당 편미분값을 빼준다.
- 오차함수의 기울기가 음수라면 편미분값도 음수이므로 편미분값을 빼면 더하기로 바뀌면서 점점 0에 가까워진다
- 반대로 오차함수의 기울기가 양수라면 편미분값도 양수이므로 편미분값을 빼면 점점 0에 가까워진다
- 계속해서 반복해 나가면 기울기와 절편값은 오차가 최소가 되도록 학습할 것이고 모델이 만들어진다
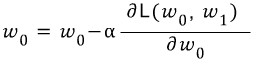
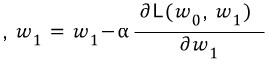
편미분값이 너무 크면 반복 횟수가 늘어나게 되고 그만큼 최적화하는 시간이 오래 걸리게 된다. α는 Learning rate라 하여 편미분값을 줄여 최적화를 돕는 역할을 한다.
'DataScience' 카테고리의 다른 글
| 기하평균의 의미 (0) | 2022.03.26 |
|---|---|
| [Pandas] Series (0) | 2021.12.30 |
| 체르노프 부등식(Chernoff Inequality) (0) | 2020.10.03 |
| 마르코프 부등식, 체비셰프 부등식 (Markov Inequality, Chebyshev Inequality) (0) | 2020.09.30 |
| [JupyterNoteBook] 시작 폴더 변경 (0) | 2020.09.21 |