[Python] 프림 알고리즘(Prim's Algorithm)

1. 프림 알고리즘(Prim's Algorithm)

프림 알고리즘은 방향이 없는 무방향 그래프에서 비용이 최소가 되는 최소 신장 트리(MST, Minimum Spanning Tree)를 찾기 위한 알고리즘이다.

 

프림 알고리즘은 그리디 알고리즘이 적용된 방법으로 임의의 노드에서 시작하여 노드를 발견할 때마다 연결된 간선 중 가중치가 가장 작은 노드의 방향으로 순회하는 알고리즘이다.

 

다음과 같은 그래프가 주어질 때 프림 알고리즘을 이용해 최소 신장 트리를 구하려 한다.

여기서는 1번 노드에서 시작해보자.

 

간선의 가중치가 최소인 13 선택

간선의 가중치가 최소인 4 선택

간선의 가중치가 최소인 3 선택

간선의 가중치가 최소인 6 선택

간선의 가중치가 최소인 9 선택

간선의 가중치가 최소인 12 선택

간선의 가중치가 최소인 11 선택

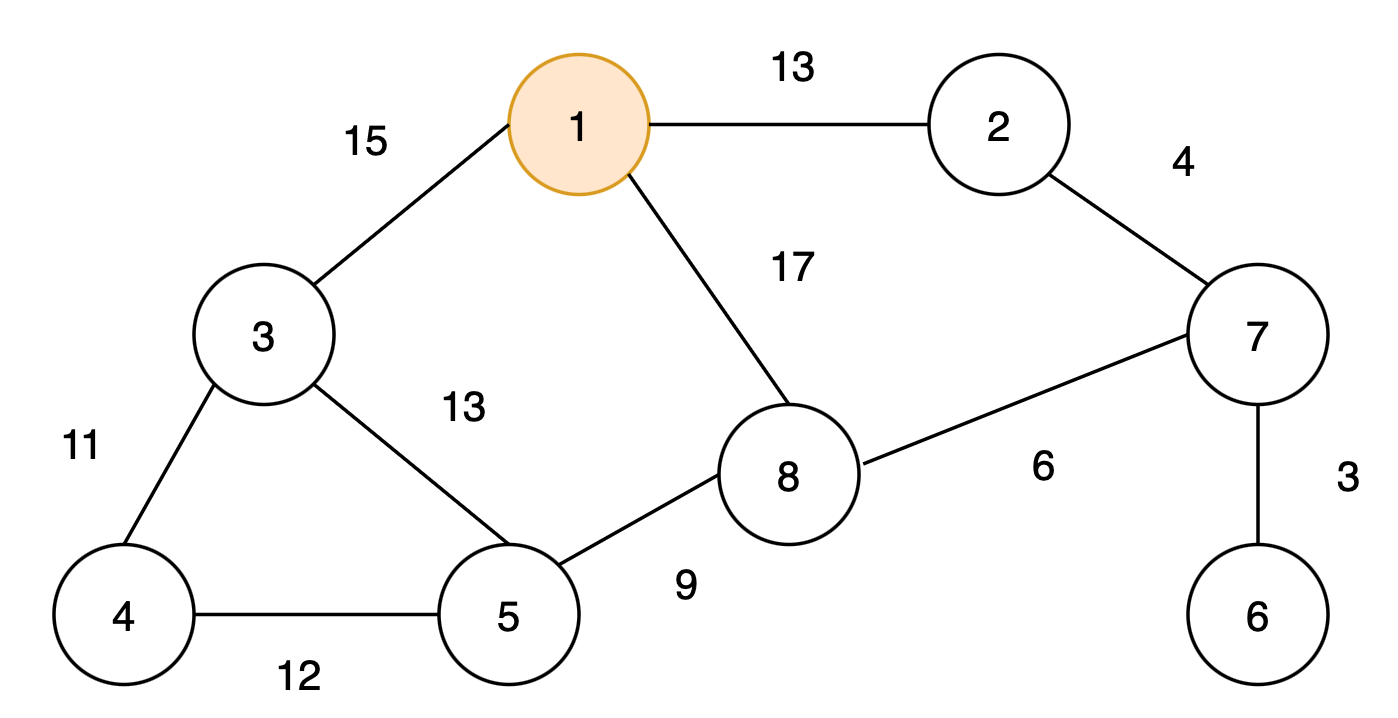
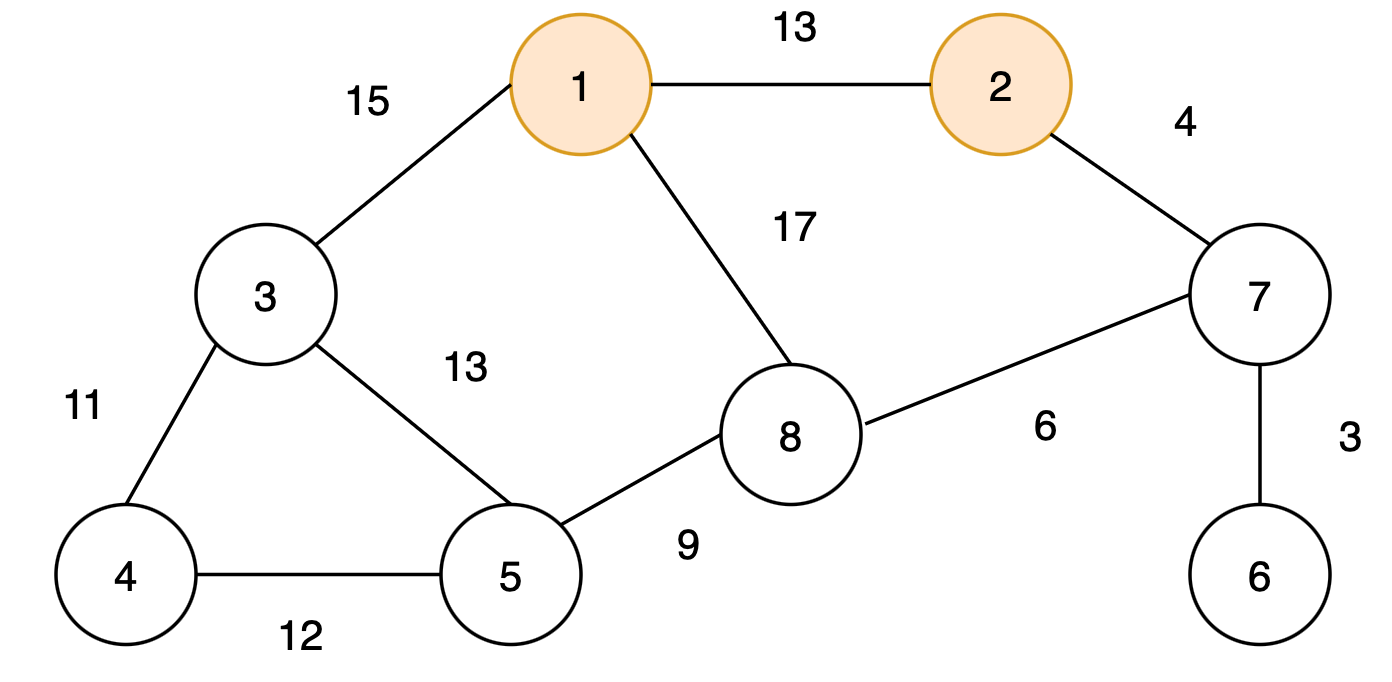
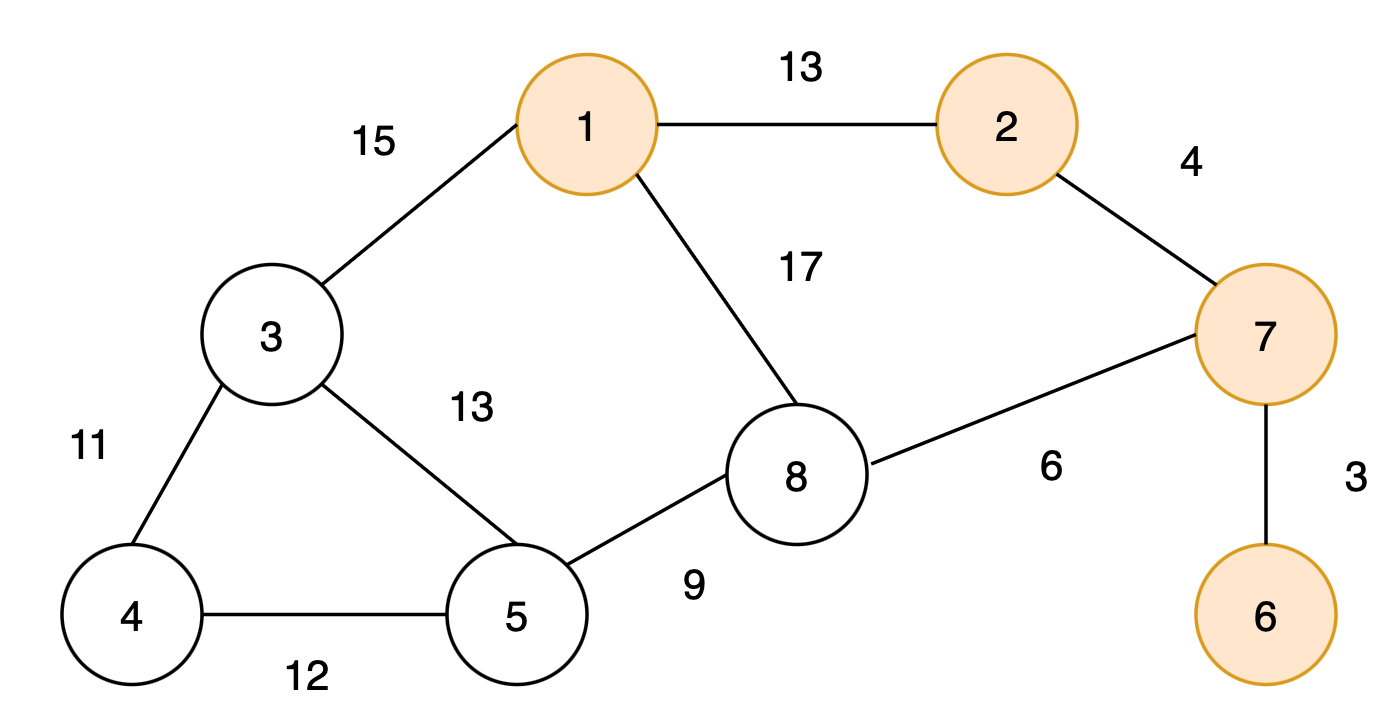
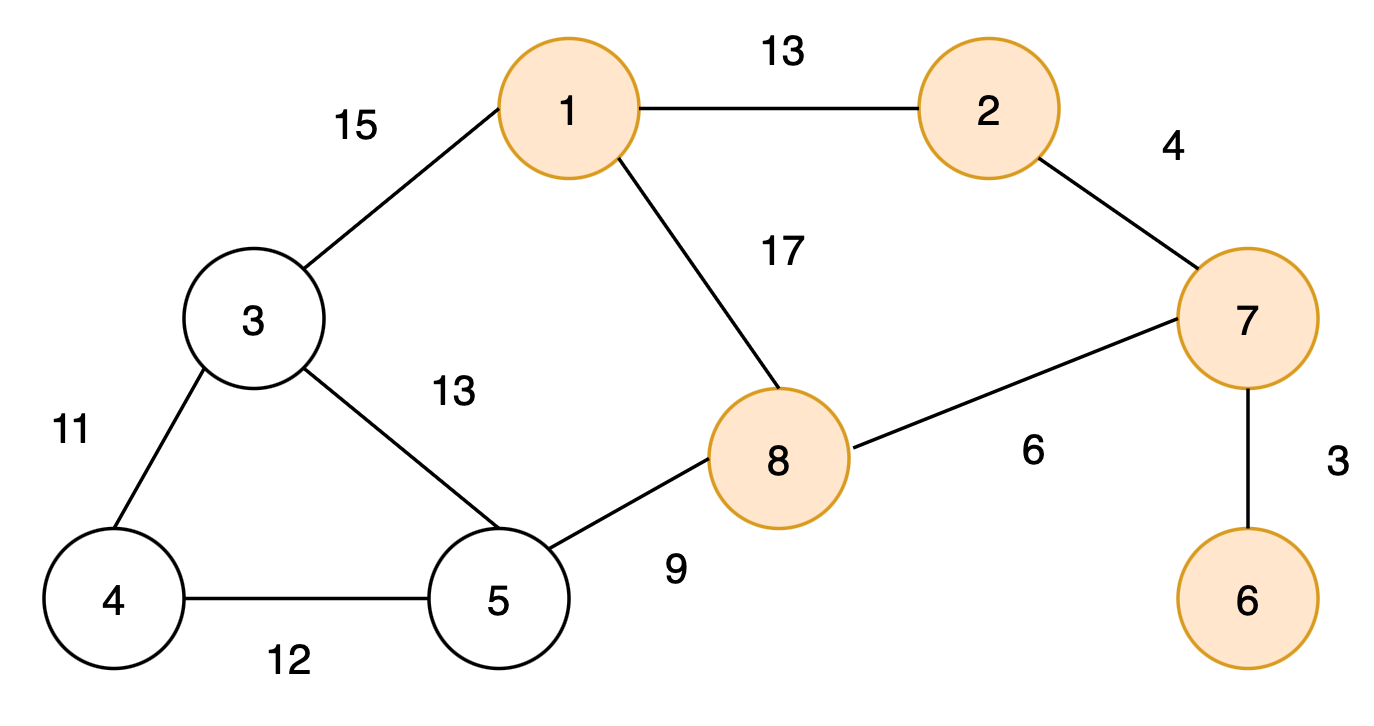
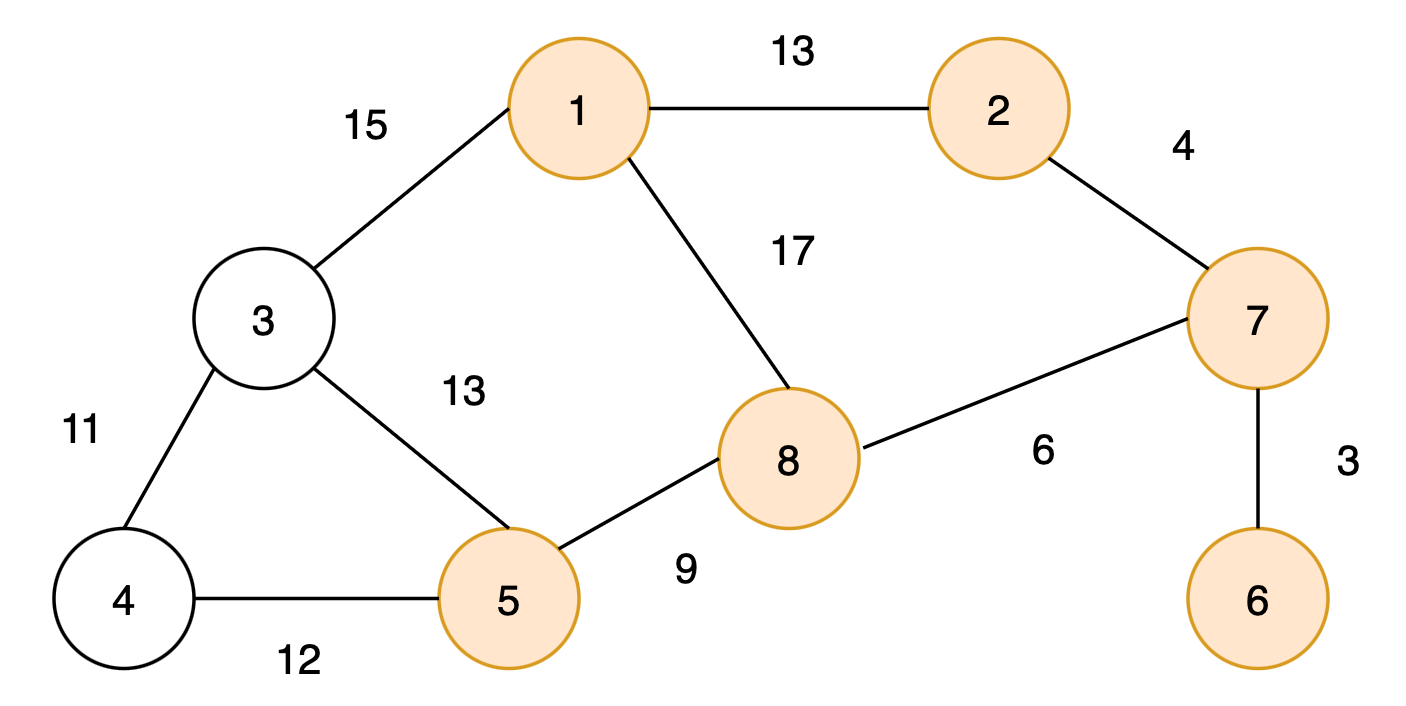
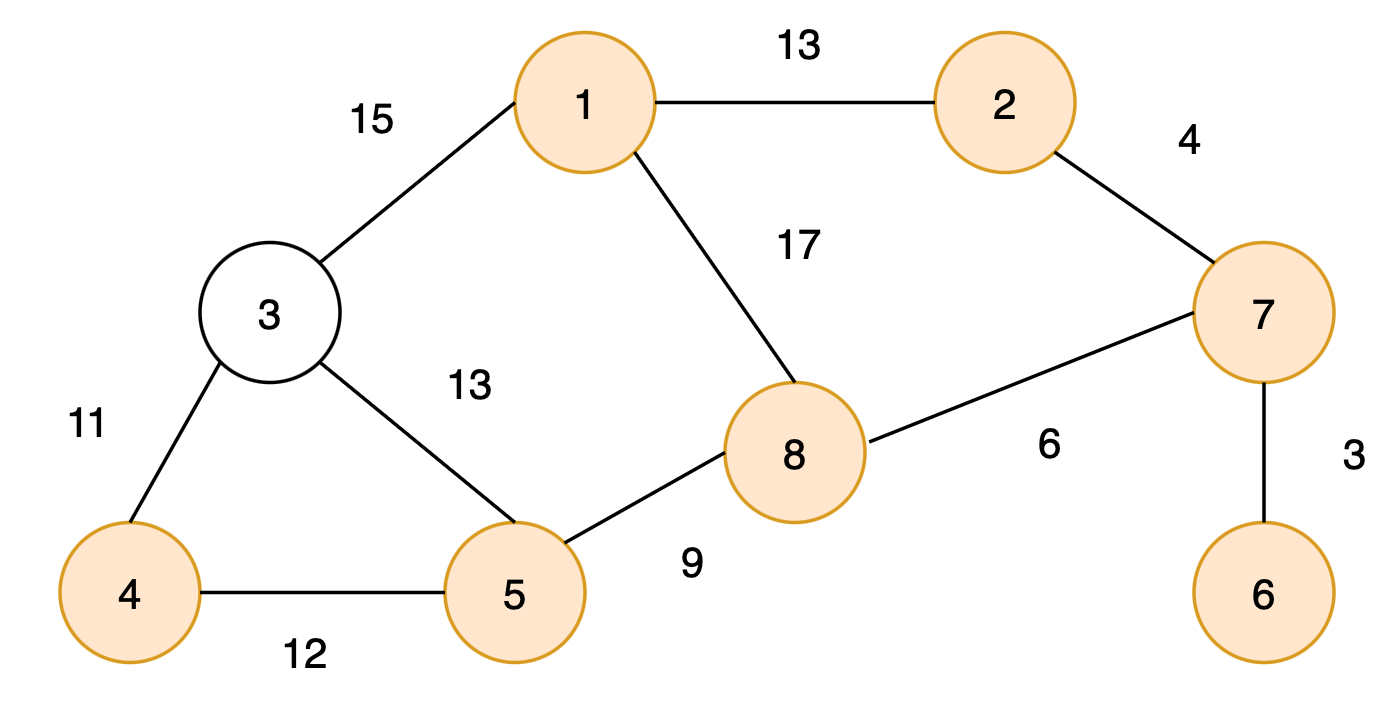
최종적으로 다음과 같은 최소 신장 트리를 구할 수 있다.

프림 알고리즘을 이용해 최소 신장 트리를 구하면 어느 위치에서 시작해도 동일한 형태의 최소 신장 트리를 구할 수 있다.

프림 알고리즘은 매번 노드가 갱신될 때마다 가중치가 최소인 간선을 선택해야 한다. 이 때 우선순위 큐를 이용해 가중치가 최소인 간선을 구하면 O(E logV)의 시간 복잡도로 최소 신장 트리를 구할 수 있다.

시간복잡도에 대한 부분은 이후 공부할 크루스칼, 다익스트라 알고리즘을 공부한 후 다시 정리해보려 한다.

2. 구현

import sys
import heapq

read = sys.stdin.readline

def prim(x):
  visited[x] = True # 시작 노드 방문
  route = [x]
  heap = graph[x] # 가중치가 최소인 간선을 선택하기 위한 최소힙(우선순위큐)
  heapq.heapify(heap) # 우선순위큐로 만들어줌
  res = 0 # 가중치를 저장할 변수
  
  while heap:
    weight, w = heapq.heappop(heap)
    if visited[w] == False:
      visited[w] = True # 방문하지 않은 노드인 경우 방문 처리
      route.append(w)
      res += weight # 가중치를 더해준다
      for edge in graph[w]:
        if visited[edge[1]] == False:
          heapq.heappush(heap, edge) # 방문여부를 판단해 아직 방문하지 않은 노드만 최소힙에 넣어줌
  return route, res
  
v, e = map(int, read().split()) # 노드의 수, 간선의 수
graph = [[] for _ in range(v + 1)] # 그래프 저장 리스트, 가중치와 종점을 저장
visited = [False] * (v + 1) # 방문 여부를 판단하기 위한 리스트

for _ in range(e):
  u, v, weight = map(int, read().split())
  # 무방향 그래프이기 때문에 시점과 종점을 모두 고려
  graph[u].append([weight, v]) # 최소힙을 사용하기 위해 가중치를 먼저 넣어준다
  graph[v].append([weight, u])

print(prim(1)) # 1번 노드에서 시작하는 경우
'''
입력:
8 10
1 2 13
1 3 15
1 8 17
2 7 4
3 4 11
3 5 13
4 5 12
5 8 9
6 7 3
7 8 6

출력:
([1, 2, 7, 6, 8, 5, 4, 3], 58)
'''