1. union-find 알고리즘
union-find 알고리즘은 서로 다른 원소가 하나의 집합에 속하는지 확인하기 위한 알고리즘이다.
서로소 집합(Disjoint-set) 알고리즘으로 서로 다른 두 노드가 같은 그래프에 속하는지 확인하는 것이 목적이다.
- 그래프에서 cycle을 형성하는지 확인하기 위해 사용
- 두 원소가 같은 집합에 속하는지 확인하기 위해 사용
2. 동작 방법

위와 같은 그래프가 주어질 때, union-find 알고리즘을 이용해 같은 부분집합에 속하는지 확인하려 한다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
union-find 알고리즘에서는 각 노드들의 부모 노드들에 대한 테이블을 생성하는데 스스로를 부모 노드로 초기화시켜준다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 1 | 4 | 5 | 6 | 2 | 8 |
3과 7의 부모 노드는 각각 1과 2이므로 부모노드를 갱신시켜준다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 1 | 3 | 3 | 7 | 2 | 8 |
나머지 노드들도 동일하게 부모 노드를 갱신시켜준다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 1 | 1 | 1 | 2 | 2 | 2 |
각 부모 노드들을 확인하여 부모노드의 부모노드가 있다면 다시 갱신시켜준다.(보통 가장 작은 숫자를 부모 노드로 설정)
최종적으로 노드 1에 속하는 부분집합과 노드 2에 속하는 부분집합으로, 그래프가 2개의 부분집합으로 구성됨을 알 수 있다.
3. 구현

def find(x):
if parent[x] != x:
return find(parent[x])
return x
def union(a, b):
a = find(a)
b = find(b)
if a < b:
parent[b] = a
else:
parent[a] = b
v, e = map(int, input().split()) # 노드 수, 간선 수
parent = [i for i in range(v + 1)] # 부모 테이블 초기화
for _ in range(e):
a, b = map(int, input().split())
union(a, b)
print('parent table: ', *parent)
'''
입력:
8 7 # 노드, 간선 수
1 3
3 4
3 5
4 5
2 7
7 8
6 7
출력:
parent table: 0 1 2 1 1 1 2 2 2
'''각 노드들의 부모 노드를 확인할 수 있다.
find 함수에 dp 방식을 적용하여 시간 복잡도를 줄이는 방법이 있다.
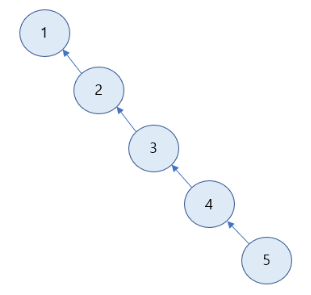
노드가 한쪽으로 치우친 경우에는 O(N)의 시간 복잡도를 갖게 된다.
find 함수에서 parent[x]의 값을 저장하는 기능을 넣어주면 union에서 루트 노드를 찾기까지 걸리는 시간 복잡도를 O(logN)으로 줄일 수 있다.
def find(x):
if parent[x] != x:
parent[x] = find(parent[x])
return parent[x]union 함수와 같이 사용할 때는 굳이 필요할까 생각을 했다.(union 함수를 사용하면서 루트 노드가 같이 갱신됨)
find 함수만 별도로 사용하는 경우에는 parent 리스트가 갱신되지 않기 때문에 union-find 알고리즘을 사용할 때는 꼭 find 함수가 parent를 갱신시켜주도록 구현하자.
'CS > 알고리즘' 카테고리의 다른 글
| [Python] CCW(Counter Clock Wise) (0) | 2023.02.06 |
|---|---|
| [Python] 프림 알고리즘(Prim's Algorithm) (0) | 2023.01.22 |
| [Python] BFS/DFS (Breadth-First Search, Depth-First Search) 구현 (0) | 2023.01.16 |
| 유클리드 호제법 (0) | 2023.01.11 |
| 배수판정법 (1) | 2023.01.10 |