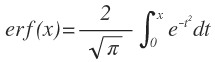Koo's.Co

1. 오차 함수 다음과 같은 함수를 오차 함수(Error Function)라 한다. 줄여서 erf라고도 한다. 2. 오차 함수와 정규분포와의 관계 오차 함수는 정규분포의 cdf와 밀접한 관계가 있는데 둘의 관계를 확인해 보려 한다. 즉, 정규분포의 cdf와 오차함수는 본질적으로 같은 함수임을 알 수 있다. 오차 함수에 값을 대입하고 평행이동을 하면 정규분포의 cdf를 구할 수 있다. 3. 그래프 확인하기 math.erf 함수를 이용하면 정규분포의 CDF를 구할 수 있다 import matplotlib.pyplot as plt import math def normal_cdf(x, mu=0, sigma=1): return (1+math.erf((x-mu)/math.sqrt(2)*sigma))/2 xs = n..

Python을 이용해 정규분포를 그려보려 한다. 정규분포의 pdf는 다음과 같다. 1. 직접 생성 위 식을 함수로 정의하면, 다음과 같다 import matplotlib.pyplot as plt import math def normal_pdf(x, mu=0, sigma=1): return(math.exp(-(x-mu)**2)/(2*sigma**2))/(math.sqrt(2*math.pi)*sigma) 다음과 같이 xs_1에 대한 정규분포를 구해보자(plot에 정수값을 넣을 수 없으므로, x/10을 대입) xs_1 = [x/10 for x in range(-50, 50)] plt.plot(xs_1, [normal_pdf(x) for x in xs_1]) 다양한 정규분포를 구해보면, plt.plot(xs, ..

1. 정규 분포의 랜덤 변수 정규 분포는 Gaussian Distribution 또는 Normal Distribution이라 한다. 고등학교 때 확률과 통계에서도 배우고 대학교에 올라와서도 제일 중요하게 배우는 분포이다. 정규분포는 중심 극한 정리나 이외에도 여러 공식을 유도할 때도 많이 사용되는 통계에서 가장 중요한 분포이다. 2. 정규분포의 특성 1) 종모양의 분포 : 좌우가 대칭인 종모양의 분포를 갖는다 2) 평균값 = 중앙값 = μ 3) P(x =μ) = 1/2 4) 평균이 0, 분산이 1인 표준 정규분포를 갖는다 5) 표준정규분포는 별도의 표가 존재해 값을 구하기 편하다 3. 평균 이 때, 앞의 식은 기함수와 우함수가 곱해져 기함수이므로, 적분 값은 0이 되고, 뒤의 식을 적분하면, 이 된다. ..

다음과 같은 적분을 가우스 적분이라 한다 가우스 적분은 중심 극한 정리에 사용되며 정규 분포 식을 증명할 때도 사용되는 적분이다. 이외에도 편미분에서도 자주 등장하는 함수로 알아두면 유용한 함수이다. 주어진 함수를 그리면 다음과 같다 import numpy as np import matplotlib.pyplot as plt def func_(x): return np.exp(-(x**2)/2) x = np.arange(-5, 5, 0.1) plt.plot(x, func_(x)) 그래프는 범위를 -5~5까지 한정했지만 그래프가 무한대로 가면 결국 양 끝은 0으로 수렴할 것이다. 해당 그래프의 범위는 어떻게 구할 수 있을까? 구하고자 하는 적분의 결과 값을 I로 두면 다음과 같다 양변을 제곱하면, 이 때, x..

1. 지수 랜덤 변수 - λ>0 에 대해 다음 확률 밀도 함수를 갖는 X를 지수 랜덤 변수라 한다 ※부분적분을 이용해 평균과 분산을 구할 수 있다 2. 평균 3. 분산

1. 푸아송 랜덤 변수 - 푸아송 랜덤 변수는 주어진 시간동안 사건이 랜덤하게 일어날 확률을 나타낸다 - 각 시행이 일어날 확률이 랜덤하므로, 일정 시간동안 평균적으로 몇 번 발생했는지를 나타낸다 - 웹 서버의 REQUEST, 방사성 물질의 입자 방출 등의 분야에서도 사용된다 ※매클로린 급수를 이용해 평균과 분산을 구할 수 있다 2. 평균 3. 분산

1. 파스칼 랜덤 변수 - 성공/실패 두 가지 결과만 나타내는 시행을 n회 반복한다 - 성공확률이 p일 때, 실패할 확률은 1-p이다 - n번 시행 중 처음으로 k번 성공하는 확률을 나타낸다 - 베르누이 시행이 독립적으로 n회 반복된다 - k가 1일 때의 파스칼 분포는 기하 분포를 의미한다 - 파스칼 분포는 기하 분포의 일반화이다 1) x-1번까지 시행의 확률 - x-1번 중 k-1번 성공, (x-1)-(k-1)=x-k번 실패할 확률이다 - 이항 분포를 따른다 2) x번째 시행의 확률 - x번째 시행에서 처음으로 k번 성공해야 하므로 x번째 시행은 성공이다 ※ iid와 기하 분포의 평균과 분산을 이용해 파스칼 분포의 평균과 분산을 구할 수 있다 2. 평균 - 랜덤 변수 X를 독립이면서 기하분포를 따르는 ..

1. 이항 랜덤 변수 - 성공/실패 두 가지 결과만 나타내는 시행을 n회 반복한다 - 성공확률이 p일 때, 실패할 확률은 1-p이다 - n번 시행 중 x번 성공하는 확률을 나타낸다 - 베르누이 시행이 독립적으로 n회 반복됨을 의미한다 조합을 이용해 n번 중 성공이 순서없이 x번 발생하는 경우의 수를 구한다 성공할 확률은 p이므로, 확률p가 x번 반복된다 실패할 확률은 1-p로, 확률1-p가 n-x번 반복된다 2. 평균 - 이항 랜덤 변수는 베르누이 시행이 독립적으로 n회 반복되는 시행을 나타낸다 - 베르누이 랜덤 변수의 평균은 p이다 베르누이분포의 정의와 평균 1. 베르누이 랜덤 변수 - 성공/실패 두 가지 결과만 나타내는 한 번의 시행을 나타낸다 - 성공확률이 p일 때, 실패할 확률은 1-p이다 X 0..

1. 베르누이 랜덤 변수 - 성공/실패 두 가지 결과만 나타내는 한 번의 시행을 나타낸다 - 성공확률이 p일 때, 실패할 확률은 1-p이다 X 0 1 계 1-p p 1 2. 평균 - 이산 랜덤 변수의 평균은 다음과 같이 구할 수 있다 - 베르누이 랜덤 변수는 항상 0 또는 1의 결과만 가지므로, 평균은 다음과 같다 3. 분산 - 이산 랜덤 변수의 평균은 다음과 같이 구할 수 있다 - 베르누이 랜덤변수의 분산을 구하면,