1. 정규분포를 표준화하는 이유
정규분포를 사용할 때는 먼저 평균과 표준편차를 ~N(0, 1)인 표준정규분포로 표준화한 후에 사용합니다.
정규분포를 따르는 분포는 많지만 각각의 평균과 표준편차가 다르기 때문에 일반화할 수 없기 때문입니다.
평균과 표준편차가 아무리 다르더라도 N(0, 1)로 만든다면 모두 같은 특성을 가지는 동일한 확률분포로 사용할 수 있습니다.
그렇다면 어떻게 이런 표준화가 가능할까요
2. 표준화하는 방법
데이터를 표준화하는 방법은 간단합니다.

지금부터 왜 이렇게 표준화가 되는지 차근차근 알아보려합니다.
[5, 7, 11, 13, 8, 4] 라는 공부시간 데이터가 있을 때 해당 자료를 정규화하려 합니다.
1) 평균
주어진 데이터는 평균으로 8을 갖습니다. 이 때 모든 데이터에 대해 평균만큼 빼고 다시 값을 구하면 평균이 0이 됩니다.
정규분포도 마찬가지로 모든 데이터에 대해 평균만큼을 빼주면 전체의 평균은 0이 됩니다.

x = [5, 7, 11, 13, 8, 4]
x = np.array(x)
np.average(x) # 8.0
np.average(x - np.average(x)) # 0.02) 표준편차
주어진 데이터는 3.16227... 이라는 표준편차를 갖습니다. 마찬가지로 모든 데이터에 대해 표준편차로 나눠준 후 다시 표준 편차를 구하면 표준편차는 1이 됩니다.

np.std(x) # 3.1622776601683795
np.std(x / np.std(x)) # 1.0이 때 먼저 표준편차로 자료들을 나누게 되면 평균값이 바뀌게 되기 때문에 먼저 자료에서 평균을 뺀 후에, 표준편차로 나눠줘야 합니다.
3. 평균과 표준편차 변화에 대한 정규분포 그래프의 변화
파이썬을 이용한 정규분포 그래프를 그리는 방법은 아래 게시물을 참고하시면 됩니다!
[Matplotlib] 정규분포 그리기
Python을 이용해 정규분포를 그려보려 한다. 정규분포의 pdf는 다음과 같다. 1. 직접 생성 위 식을 함수로 정의하면, 다음과 같다 import matplotlib.pyplot as plt import math def normal_pdf(x, mu=0, sigma=1..
koosco.tistory.com
import matplotlib.pyplot as plt
import scipy.stats as st
import numpy as np
xs = np.arange(-5, 5, 0.1)
plt.plot(xs, st.norm.pdf(xs, loc=0, scale=1), 'r')
plt.plot(xs, st.norm.pdf(xs, loc=1, scale=1), 'b')
표준편차가 동일할 때 평균이 변하게 되면 그래프는 x축 평행이동만 하게 되고 그래프의 모양은 동일하게 유지됩니다.
표준화를 할 때 데이터에서 평균을 빼는 과정은 그래프의 중심을 0으로 이동하는 과정이 됩니다.
plt.plot(xs, st.norm.pdf(xs, loc=0, scale=1), 'r')
plt.plot(xs, st.norm.pdf(xs, loc=0, scale=1.5), 'b')
plt.plot(xs, st.norm.pdf(xs, loc=0, scale=0.5), 'g')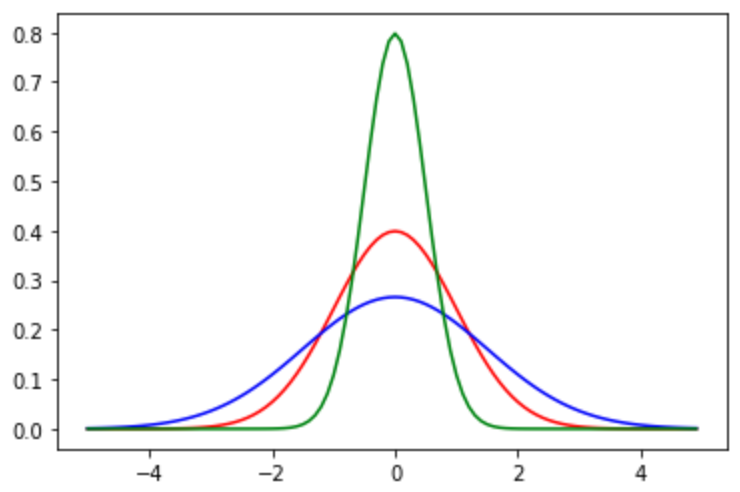
표준편차로 데이터를 나누는 과정은 그래프의 모양을 표준편차가 1인 모양으로 바꿔주는 과정입니다.
표준편차가 1보다 더 크다면 그래프는 표준정규분포보다 더 낮고 넓게 퍼지게 되고,
표준편차가 1보다 더 작다면 그래프는 표준정규분포보다 더 높고 좁게 퍼지게 됩니다.
표준화하는 과정은 더 넓거나 좁은 정규분포의 모양을 표준 정규분포 형태로 변환하는 과정입니다.
'DataScience' 카테고리의 다른 글
| 모집단과 표본집단, 표본평균의 의미 (0) | 2022.07.07 |
|---|---|
| [Numpy] 다항식을 다룰 수 있는 polynomial class, poly1d (0) | 2022.06.15 |
| 통계적 추론, 추정의 의미? (0) | 2022.06.07 |
| 기하평균의 의미 (0) | 2022.03.26 |
| [Pandas] Series (0) | 2021.12.30 |