이전에 c++를 사용해 행렬곱을 구현한 적이 있었다.
파이썬에서는 numpy 라이브러리를 이용하면 간단하게 행렬곱을 구할 수 있다.
- 다음과 같이 A와 B가 주어질 때,
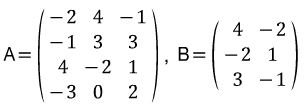
행렬곱의 결과는 다음과 같다

1. numpy.matmul
|
import numpy as np A=[[2,4,-1],[-1,3,3],[4,-2,1],[-3,0,2]] B=[[4,-2],[-2,1],[3,-1]] result=np.matmul(A,B) print(result) |
matmul 함수에 행렬 A와 B를 넣으면 행렬곱을 구할 수 있다.

하지만 행렬에 스칼라곱을 하면 에러가 발생한다.
|
import numpy as np
A=[[2,4,-1],[-1,3,3],[4,-2,1],[-3,0,2]] B=3 result=np.matmul(A,B) print(result) |

2. numpy.dot
|
import numpy as np from numpy import dot
A=[[2,4,-1],[-1,3,3],[4,-2,1],[-3,0,2]] B=[[4,-2],[-2,1],[3,-1]] result=dot(A,B) print(result) |

|
import numpy as np
A=[[2,4,-1],[-1,3,3],[4,-2,1],[-3,0,2]] B=3 result=np.dot(A,B) print(result) |

-dot함수를 이용하면, 두 행렬을 입력하면 행렬곱을, 행렬과 스칼라를 입력하면 스칼라곱을 반환한다.

※numpy의 dot함수는
1. 1차원 배열 2개를 매개변수로 받으면 두 벡터의 내적을 반환
2. 2차원 배열 2개를 매개변수로 받으면 두 행렬의 행렬곱을 반환
3. 둘 중 하나가 0차원 배열(스칼라)이면 스칼라곱을 반환
4. 두 번째 매개변수가 1차원 배열이면 열벡터로 계산한다
'Math > Linear Algebra' 카테고리의 다른 글
| 행렬의 고유값/고유벡터 (0) | 2020.07.05 |
|---|---|
| 행 사다리꼴, 기약 행 사다리꼴 (0) | 2020.07.01 |
| 가우스-조단 소거법 (1) | 2020.07.01 |
| 선형대수 개요 (0) | 2020.05.07 |
| 행렬의 곱셈 (0) | 2020.04.21 |