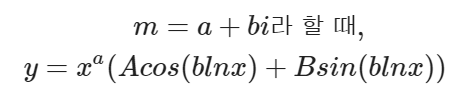1. 오일러-코시 방정식(Euler-Cauchy Equation)
1) 2계 오일러-코시 방정식

오일러-코시 방정식을 사용하면 위와 같은 형태의 미분방정식을 풀 수 있습니다.
이 때의 일반해를 x에 대한 지수배로 정의하여 풀이할 수 있습니다.

x에 대해 미분할 때마다, 차수가 하나씩 줄어드는 성질을 이용해 특성방정식을 구해 문제를 풀 수 있습니다.

구해진 특성 방정식을 이용해 해를 구할 수 있습니다.
2) 3계 오일러-코시 방정식

3계 오일러-코시 방정식도 2계 오일러-코시 방정식과 동일한 방식으로 특성방정식을 구할 수 있습니다.
특성방정식을 구하면 다음과 같습니다.

동일한 방식으로 n계 오일러-코시 방정식까지 방정식을 확장할 수 있습니다.
2. 예제
1) 서로 다른 두 실근

일반해를 구하면 다음과 같습니다.

2 중근

중근을 갖는 경우에는 앞서 상수계수 2계 미분방정식을 풀 때와 동일하게 차수 축소법을 사용해 다른 해를 구할 수 있습니다. 중근을 가질 때의 일반해를 구하면 다음과 같습니다.

3) 허근

약간의 트릭을 사용하면 오일러 공식을 사용할 수 있도록 식을 바꿔줄 수 있습니다.

이를 일반화하여 일반해를 나타내면 다음과 같습니다.